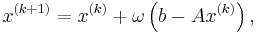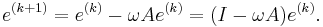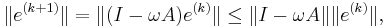Modified Richardson iteration
Modified Richardson iteration is an iterative method for solving a system of linear equations. Richardson iteration was proposed by Lewis Richardson in his work dated 1910. It is similar to the Jacobi and Gauss–Seidel method.
We seek the solution to a set of linear equations, expressed in matrix terms as
The Richardson iteration is
where  is a scalar parameter that has to be chosen such that the sequence
is a scalar parameter that has to be chosen such that the sequence 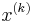 converges.
converges.
It is easy to see that the method is correct, because if it converges, then 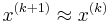 and
and 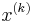 has to approximate a solution of
has to approximate a solution of  .
.
Convergence
Subtracting the exact solution  , and introducing the notation for the error
, and introducing the notation for the error 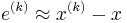 , we get the equality for the errors
, we get the equality for the errors
Thus,
for any vector norm and the corresponding induced matrix norm. Thus, if 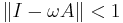 the method convergences.
the method convergences.
Suppose that  is diagonalizable and that
is diagonalizable and that 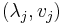 are the eigenvalues and eigenvectors of
are the eigenvalues and eigenvectors of  . The error converges to
. The error converges to 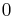 if
if 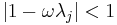 for all eigenvalues
for all eigenvalues 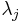 . If, e.g., all eigenvalues are positive, this can be guaranteed if
. If, e.g., all eigenvalues are positive, this can be guaranteed if  is chosen such that
is chosen such that 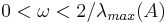 . The optimal choice, minimizing all
. The optimal choice, minimizing all 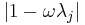 , is
, is 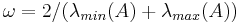 , which gives the simplest Chebyshev iteration.
, which gives the simplest Chebyshev iteration.
If there are both positive and negative eigenvalues, the method will diverge for any  if the initial error
if the initial error 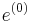 has nonzero components in the corresponding eigenvectors.
has nonzero components in the corresponding eigenvectors.
References
- Richardson, L.F. (1910). "The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam". Philos. Trans. Roy. Soc. London Ser. A 210: 307–357.
- Vyacheslav Ivanovich Lebedev (2002). "Chebyshev iteration method". Springer. http://eom.springer.de/c/c021900.htm. Retrieved 2010-05-25. Appeared in Encyclopaedia of Mathematics (2002), Ed. by Michiel Hazewinkel, Kluwer - ISBN 1402006098
|
||||||||||||||